彩色数と次数の定理（グラフ理論）

数学のグラフ理論で、グラフの彩色数と頂点の次数に関する定理を発見したのでブログで公開することにしました。
もしかすると、この定理はすでに世の中に存在するのかもしれません。
その場合は、コメント欄からご指摘ください。

彩色数

彩色数とは、グラフ \(G\) を点彩色するときに最低限必要な色の数のことです。
記号では、\( \chi(G) \) と書きます。
例えば、下のようなグラフでは、\( \chi(G) = 4 \) となります。

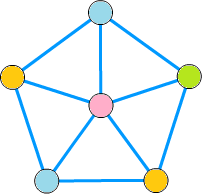
次数

次数とは頂点に接続している辺の本数のことです。
頂点 \( v \) の次数を \( deg(v) \) と書きます。
下のグラフでは、ラベルの数字がその頂点の次数を表しています。

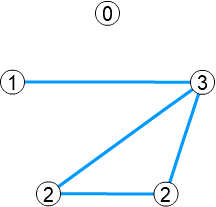
彩色数と次数の定理

それでは、私が発見した「彩色数と次数の定理」をご紹介します。
それは、次のようなものです。

\( \chi(G) = k \) のグラフ \( G \) において、\( deg(v) < k-1 \) の頂点 \( v \) を辺ごと削除しても、\( G \) の彩色数は変わらない。

これは、「彩色数が \( k \) であるグラフは、次数が \( k-1 \) 以上の頂点だけで表せる」ことを意味しています。

具体例を用いて確認してみましょう。
以下は、彩色数が \( 4 \) のグラフです。

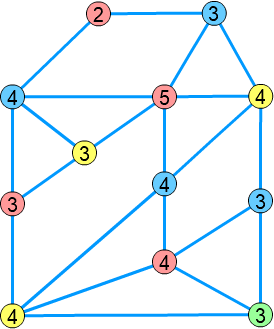
定理によれば、彩色数が \( 4 \) のグラフでは、次数 \( 3 \) 未満の頂点を辺ごと削除しても彩色数は変わらないはずです。
グラフの左上に次数 \( 2 \) の頂点があるので、これを削除してみましょう。

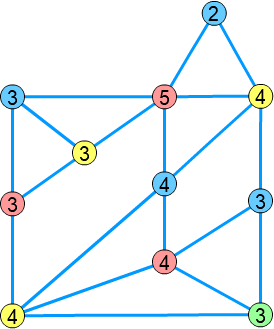
すると、このようになります。
グラフの彩色数は相変わらず \( 4 \) のままですね。

頂点を一つ削除したことにより、右上の頂点の次数が \( 2 \) になりました。
こちらも削除してしまいましょう。

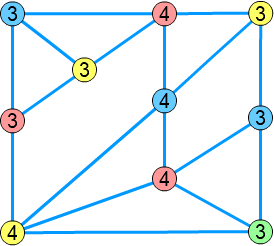
このようにして、グラフから次数 \( 3 \) 未満の頂点をすべて削除することができました。
グラフの彩色数は \( 4 \) のままであることを確認してみてください。

定理の証明

背理法を用いて証明します。

\( \chi(G) = k \) のグラフ \( G \) において、\( deg(v) < k-1 \) の頂点 \( v \) を辺ごと削除した時、新たにできたグラフ \( G’ \) の彩色数が \( \chi(G’) = k-1 \) に減少したとします。

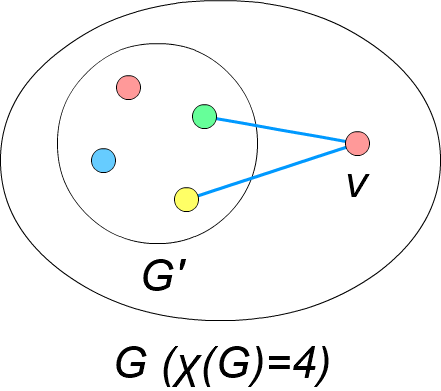
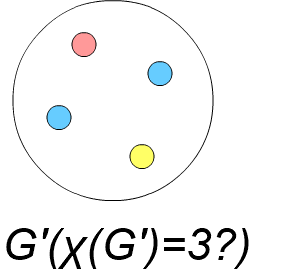
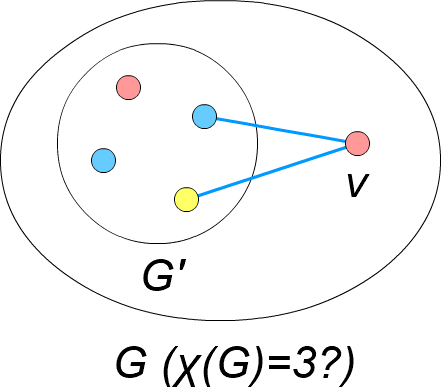
この時、\( G’ \) を \( k-1 \) 色で点彩色し、削除した頂点 \( v \) を辺ごと元に戻します。
すると、\( deg(v) < k-1 \) なので、\( v \) も必ず \( k-1 \) 色で彩色できるはずです。
その結果、\( G \) 全体が \( k-1 \) 色で点彩色できてしまい、\( \chi(G) = k \) であることに矛盾します。(証明終)