前回の記事では、
・四色問題(四色定理)とは何か?
・塗り絵パズルのコツ
・四色問題の歴史
について触れました。
まだ、読まれていない方は、まずそちらの記事からお読みになってくださいね。
さて、今回から実際に四色問題の証明に入るのですが、
証明を行うためには、いくつかの予備知識が必要になりますので、
まずはそれらの用語や定理について解説したいと思います。
■ 四色問題の証明に必要な予備知識
▼ 双対グラフ(そうついぐらふ)
四色問題の証明を考える際、実際の塗り絵や地図を使って考えると分かりにくいんですよ。
そこで、「双対グラフ」というものを利用して、色の塗り分けを考えていきます。
双対グラフとは、塗り絵の中の面を頂点に置き換え、隣り合う面同士は頂点を辺で結ぶことで表したグラフのことです。
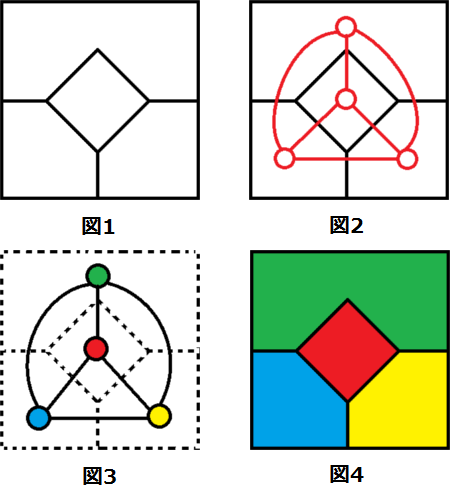
具体例を挙げると、たとえば上のような塗り絵があったとします。(図1)
この塗り絵の中の面に頂点を対応させ、隣り合う面は辺で結びます。(図2)
こうしてできた双対グラフに対し、辺で結ばれた頂点は互いに異なる色になるように塗り分けます。(図3)
頂点の塗り分けができた双対グラフを元に戻せば、見事に塗り絵が完成します。(図4)
双対グラフがいかに便利なものか、ご理解いただけたでしょうか。
この双対グラフを用いることで、
「地図上の隣り合う国を異なる色で塗る」
という問題を、
「グラフ上の辺で結ばれた頂点を異なる色で塗る」
という問題に置き換えて考えることができるようになるのです。
以下、四色問題の証明は、この双対グラフを用いて話を進めていきます。
▼ 平面グラフと平面的グラフ
平面グラフとは、頂点以外で辺が交わらないグラフのことです。
平面的グラフとは、頂点以外で辺が交わっているが、辺を動かして平面グラフに描き直すことができるグラフです。
ちなみに、グラフ理論ではグラフを描くことを「埋め込む」というので、以下この言葉を使用していきます。
それでは早速具体例を見ていきましょう。
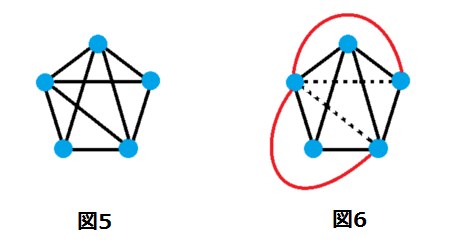
上のグラフは頂点以外で辺が交わってしまっていますので、平面グラフではありません。(図5)
しかし、交わっている辺を(頂点にくっ付けたまま)うまく動かしてあげれば…
平面グラフに埋め込むことができました!(図6)
辺を動かすときのポイントですが、辺がゴムのような柔らかい素材でできていると考えるとイメージしやすいと思います。
ですので、図5は平面グラフではないが、平面的グラフではあったわけです。
では、次のグラフはどうでしょうか?(図7)
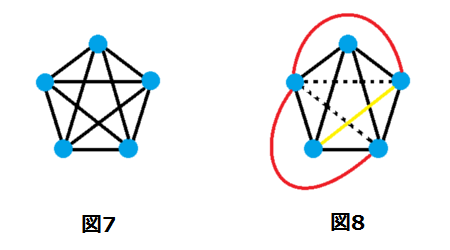
これは、最後の1本(黄色の辺)をどのように動かしても他の辺と交わってしまうので、平面グラフに埋め込むことができません。(図8)
したがって、このグラフは平面的グラフではないことが分かります。
ここで重要なポイントは、
塗り絵や地図の双対グラフは、平面グラフになるということです。
なぜかと言えば、
「塗り絵や地図は平面だから」
です。
ですので、
「どんな塗り絵や地図も4色で塗り分けられるか?」
という問題は、
「どんな平面グラフの頂点も4色で塗り分けられるか」
という問題に置き換えて考えることができるのです。
▼ オイラーの多面体定理
オイラーの多面体定理とは、以下のような定理です。
というものです。
そして、このオイラーの多面体定理は、平面グラフの頂点や辺、面についても成立します。
それでは、実際に証明してみましょう。
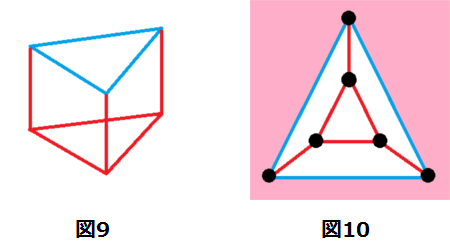
ここに、左上のような三角柱があったとします。(図9)
この三角柱を平面グラフに埋め込むと右上の図のようになります。(図10)
ここで注意してほしいのは、グラフの一番外側(図のピンクの部分)も一つの面と考えるということです。
立体を無理やり平面にしたので、底面が外側にはみ出してしまったのですね。
ちなみに、このピンクの面はどのような形をしているか分かりますか?
答えは、
「三角形」です!
なぜかというと、頂点が3つ、辺が3本(水色の部分)ありますからねぇ。(そんな…)
この、「外側の領域も一つの面である」という考え方は超重要ですので、しっかり押さえておいてください。
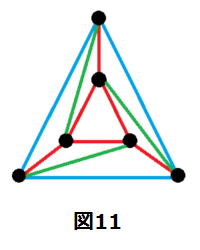
次に、どのような多面体でも同じ議論ができるように、平面グラフの面をすべて三角形に分割します(緑の辺)。(図11)
「え!? そんなことしてもいいの?」
という気がしますが、辺を1本引くと面も1つ増えるので、「頂点-辺+面」の値は変わらないのです。
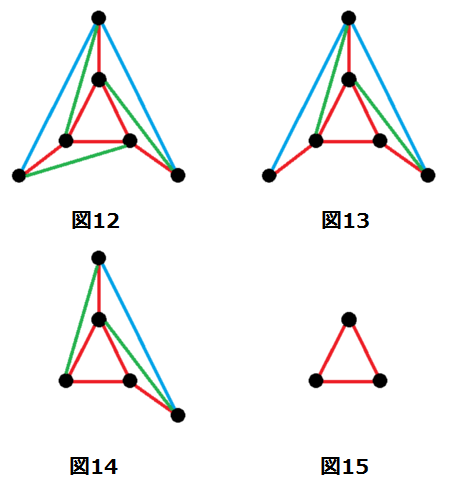
ここまで準備が整ったら、外側の三角形から順番に消していきます。
まずは下の水色を消してみました。(図12)
辺が1つ減りますが、面も1つ消えたので、「頂点-辺+面」の値は変わりません。
次に緑を消しました。先ほどと同じく、辺と面が1つずつ消えた形になっています。(図13)
今度は、左の三角形を消しました。(図14)
辺が2本(水色と赤色)減りましたが、頂点と面も1つずつ減ったので、やはり「頂点-辺+面」の値は変わりません。
以下、同様の作業を続けます。
すると、最終的に平面グラフはたった1つの三角形になってしまいます。(図15)
このとき、
頂点-辺+面 = 3 – 3 + 2(外側も面に含めるのでしたね)= 2
が成立するのです。
ちなみに、さらに辺や頂点を消去していって、最後はたった1つの頂点になったとしても、式は成り立つので、この定理の奥深さを感じます。
以上、四色問題の証明に必要な予備知識についてのお話でした。
次回は、いよいよ四色問題をエレガントに証明(します)したいです。