グラフ理論において、あるグラフが平面的であるかどうかを見極めるための重要な定理、
クラトフスキーの定理
の証明第4弾です。
前回までの記事を読まれていない方は、まずそちらからご覧ください。
さて、今回は前回証明した従属命題を用いて、最小の非平面的グラフが3-連結であることを証明していきます。
■ 最小の非平面的グラフが 3-連結 であることの証明
□ その時、\(G\) は 3-連結になる。
▽ 証明
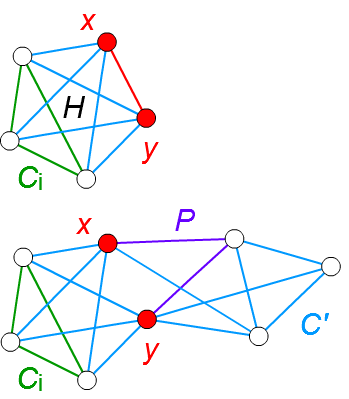
□ 最小の非平面的グラフ \(G\) が 3-連結でない、すなわち 2-連結 であると仮定します。
□ \(G\) を \(x,y\) で切断した非連結グラフの連結成分を \(C_1,\cdots,C_k\)とします。
□ 前回証明した従属命題より、\(C_i\) と \(x,y\) の誘導部分グラフに辺 \(xy\) を加えたものが非平面的になるような \(C_i\) が存在します。
その非平面的グラフを \(H\) とします。
□ 辺 \(xy\) が \(G\) に属すると、\(G\) は \(H\) を部分グラフとして含むことになり、\(G\) が最小の非平面的グラフであることに矛盾します。
したがって、\(G\) は辺 \(xy\) を含みません。
□ \(G\) を \(x,y\) で切断した非連結グラフの別の連結成分を \(C’\) とします。
□ \(G\) において、\(x\) と \(y\) の間に、\(C’\) の頂点のみを使用したパス \(P\) が存在します。
□ \(C_i\) と \(x,y\) の誘導部分グラフを \(P\) と結合すると、\(H\) の細分ができてしまいます。
この細分から、\(C’\) 上の頂点を取り除いても(頂点だけ消す)非平面的グラフ( \(H\) )になるため、
\(G\) が最小の非平面的グラフであることに矛盾します。
■ 縮約
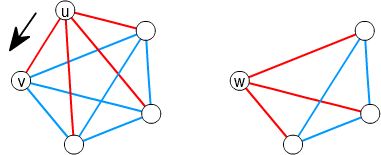
グラフにおいて、2つの頂点 \(u,v\) の間にある辺をどんどん縮めていき、
最終的に2点を合体させることを 縮約 といいます。
合体前の頂点に接続していた辺は、合体後の頂点 \(w\) に接続させます。
■ 拡逆(かくぎゃく)
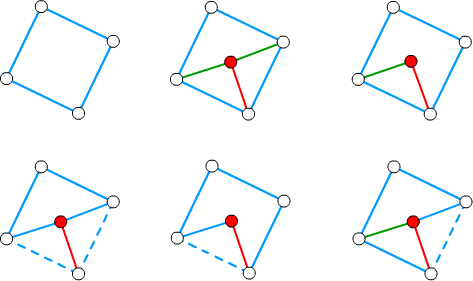
縮約の反対の操作のことです。
つまり、グラフにおいて、1つの頂点から辺で接続された頂点を伸ばしていき、
複製元の頂点と隣接した 0個以上の頂点と辺で結ぶことです。
あるいは、複製元の頂点から 0本以上の辺を奪うこともあります。
細分は拡逆の特殊なケースと考えることができます。
グラフ理論において、「拡逆」という言葉は存在しないのですが、
説明がしやすいように私が作った造語です。
■ 証明の流れ
ここまでで、クラトフスキー部分グラフを含まない非平面的グラフは 3-連結であることを示しました。
次に、そのようなグラフは平面的グラフになってしまうことを証明するのですが、
その準備として、以下の2つの従属命題を証明します。
■ 縮約によってクラトフスキー部分グラフが生じないことの証明
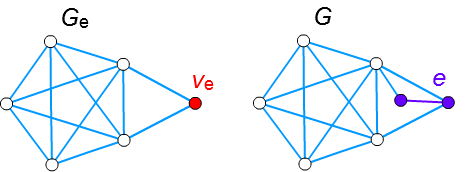
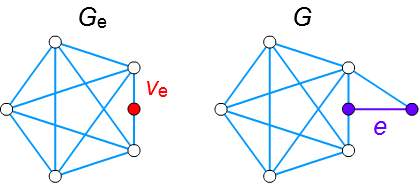
□ グラフ \(G\) の中の辺 \(e\) を縮約して得られたグラフを \(G_e\)、縮約してできた頂点を \(v_e\) とします。
□ もし、\(v_e\) がクラトフスキー部分グラフ \(H\) の中になければ、
\(H\) は縮約前から \(G\) の部分グラフであったことになり、矛盾します。
□ もし、\(v_e\) が \(H\) の辺上にあるとき、\(v_e\) を拡逆しても \(H\) となり、やはり矛盾します。
■ まとめ
いや~、1つの定理を証明するのに、一体いくつの従属命題を証明しなければならないんだろうといった感じです。
しかも、「拡逆」などという用語まで飛び出すし…。
もしかしたら、縮約の反対の操作を表す用語がすでに存在するかもしれません。
ご存じでしたら、コメント欄からご指摘いただければと思います。
ご存じでなかったら、是非この言葉を使ってあげてください(笑)
証明もいよいよ終盤に突入です。
引き続き、よろしくお願いいたします。