グラフ理論において、あるグラフが平面的であるかどうかを見極めるための重要な定理、
クラトフスキーの定理
の証明第2弾です。
まだ第1弾を読まれていない方は、まずそちらからご覧ください。
さて、今回からいよいよ証明の説明に入っていきます。
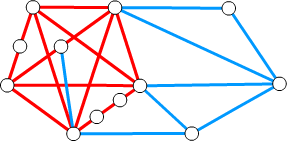
■ クラトフスキー部分グラフ
クラトフスキー部分グラフ とは、\(K_5\) や \(K_{3,3}\) の細分である部分グラフのことです。
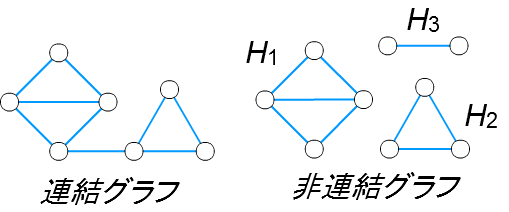
■ 連結
グラフのどの2頂点も、いくつかの辺でつながっているとき、そのグラフは 連結 であるといいます。
連結であるグラフを 連結グラフ 、そうでないグラフは 非連結グラフ と呼びます。
非連結グラフ \(G\) は、いくつかの連結グラフ \(H_1,H_2,H_3,\cdots \) に分かれており、それらを \(G\) の 連結成分 といいます。
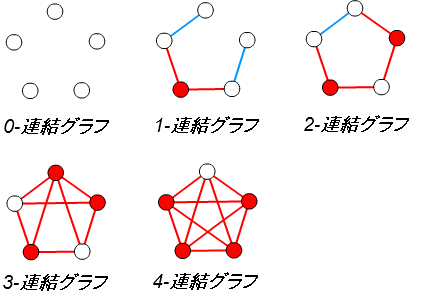
■ 点連結度
グラフ \(G\) を非連結にするために、最小で何個の頂点を取り除かなければならないかを表す数値です。
点連結度が \(k\) 以上のグラフを k-連結グラフ といいます。
頂点を取り除くときは、その頂点に接続した辺も一緒に取り除きます。
また、ハミルトンサイクル(グラフのすべての頂点を1回ずつ通るサイクル)が存在するグラフの点連結度は2以上になります。
なぜなら、輪の形で並んだ頂点は、1個取り除いただけでは非連結にできないからです。
さらに、グラフの点連結度は、グラフの頂点の中で次数が最小である頂点の次数以下となります。
なぜなら、ある頂点に接続している辺をすべて取り除けば、その頂点が孤立するのは明らかだからです。
■ 証明の流れ
クラトフスキーの定理を証明するためには、あらゆる非平面的グラフがクラトフスキー部分グラフを含むことを証明する必要があります。
しかし、実際は最小の非平面的グラフに対してのみこれを証明すれば十分です。
なぜなら、最小の非平面的グラフがクラトフスキー部分グラフを含んでいれば、
そうでない非平面的グラフも当然それを含むことになるからです。
証明の流れとしては、
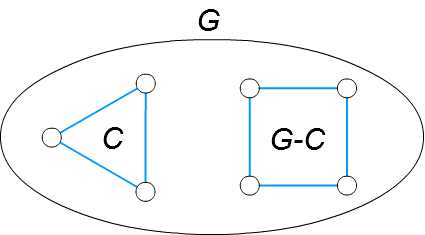
■ 最小の非平面的グラフが 1-連結 であることの証明
□ 最小の非平面的グラフ \(G\) が 1-連結でない、すなわち非連結であると仮定します。
□ \(G\) の連結成分の1つを \(C\) とします。
□ \(G\) は最小の非平面的グラフなので、たとえ1つでも頂点や辺を取り除くと、平面的になります。
その結果、\(C\) も \(G-C\) も平面的となり、\(G\) 全体も平面に描くことができるので、
\(G\) が非平面的であることに矛盾します。
■ まとめ
今回の記事も、大部分を用語の説明に使ってしまいました。
お気づきの方もいるかもしれませんが、クラトフスキーの定理の証明は、
いくつもの従属命題の証明から成り立っています。
私が初めてこの定理を学んだとき、その証明の壮大さに感銘を受けました。
次回も分かりやすい解説に努めますので、引き続きよろしくお願いいたします。