化学を勉強している高校生の中には、
「酢酸の分子量がわからない」(>_<)
ということで悩んでいる人が結構いるようです。
(ちなみに、「酢酸の化学式がわからない」という人もいます)
そこで今回は、酢酸の化学式をもとに、酢酸の分子量を計算する方法をわかりやすく解説したいと思います。
酢酸の分子量の求め方。化学式から計算する方法をわかりやすく解説
分子量とは
酢酸の分子量を計算する前に、まず、
「分子量とは何か」
という所から理解していきましょう。
質量数とは
物質は、原子という小さい粒が集まってできているのですが、
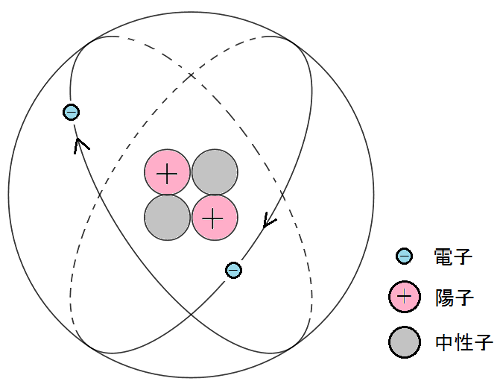
この原子は原子核の周りを電子が取り囲むような構造をしています。
この原子核は陽子と中性子というさらに小さな粒からできていて、
これらは電子よりも1800倍ぐらい重いので、原子の質量は、ほとんど原子核の質量と考えてよいわけです。
そこで、原子の質量を考えるとき、この陽子と中性子の数の和に注目し、
これを質量数とよびます。
相対質量とは
原子の質量を扱うとき、
「1個あたり何グラム」
と考えてしまうと、数値が小さすぎてわかりづらくなってしまいます。
(原子1個は、1gを1億に分けて、それをさらに1億に分けたものより軽いですから)
そこで、
「質量数が12の炭素原子 \( ^{12}_{6}C \) 1個の質量を12」
とした相対質量を用いることにしたんですね。
この相対質量を使えば、炭素原子の2倍の質量がある原子の相対質量は、
$$ 12 \times 2 = 24 $$
となり、非常に扱いやすくなるのです。
原子量とは
このように、原子の質量を相対質量で表すと大変便利なんですが、
自然界には、同じ種類の元素でも質量数が異なる同位体が存在します。
例えば、塩素原子の場合、質量数が35の原子が75%、質量数37の原子が25%、自然界に存在します。
これは、「塩素原子を100個集めると、そのうちの75個は質量数が35で、残りの25個は質量数が37である」という意味です。
ですので、自然界での存在比をもとにした質量数の平均値を考え、これを原子量といいます。
先ほどの塩素の場合で原子量を計算してみると、
$$ 35 \times 0.75 + 37 \times 0.25 = 35.5 $$
となりますね。
このように原子量を求めておけば、同位体を考えずに質量の計算ができて楽になるわけです。
分子量とは
たとえば、水の粒子は水素原子2個と酸素原子1個でできています。
このように複数の原子が結合してできた粒子を分子といい、
分子の相対質量のことを分子量と呼びます。
酢酸の分子量の計算
ここまでで分子量については理解できたと思うので、さっそく酢酸の分子量を計算してみましょう。
まず、酢酸の化学式は、
$$ C_{2}H_{4}O_{2} $$
です。
原子の結合順序がわかるように書いた示性式で表した場合は、
$$ CH_{3}COOH $$
となります。
いずれにしても、炭素原子が2個、水素原子が4個、酸素原子が2個、結合した構造であることに変わりありません。
今回は、各原子の原子量を、\( C=12.0, H=1.0, O=16.0 \) とします。
(テストの問題にも原子量は書いてありますが、基本的な原子の原子量は覚えておくとよいでしょう。)
これを用いて酢酸の分子量を計算してみると、
$$ C_{2}H_{4}O_{2} = C \times 2 + H \times 4 + O \times 2 = 12.0 \times 2 + 1.0 \times 4 + 16.0 \times 2 = 60.0 $$
となり、酢酸の分子量は「約60」であることがわかりました。
まとめ
いかがでしたでしょうか。
酢酸の分子量を計算するというのが今回の目的でしたが、
その過程において、
質量数、相対質量、原子量、分子量
といった数々の用語が出てきました。
単に分子量を丸暗記するだけではすぐに忘れてしまいます。
きちんと自分で計算できるように、言葉の意味や計算法を基本から理解していきましょう。
それでは、化学のお勉強頑張ってください。
どうもありがとうございました!
おすすめの記事