むか~し、昔、筆者は大学の理系学部の学生でした。
理系の学部の特徴として、
「レポートがめっちゃ多い」
というのがあります。
講義で教授から課されるちょっとしたものから、
実験の本格的なレポートまで、
それはそれはたくさんのレポートを書かされました。
それで、渾身の力で書き上げたレポートを提出すると、こう返ってくるんです。
「有効数字を意識してください(再提出)」
と。
「うぉおおおおおおーー!有効数字って何だーー? そんなの学校で習ってねーぞーー!!」
と、当時の私は随分困ったものでした。
今回は、昔の私のように、有効数字でお悩みの方を対象に、
などについて解説いたします。
この機会に、物理や化学の計算で必須の有効数字の丸め方をぜひマスターしてください。
有効数字とは?物理で必須の掛け算や四捨五入の仕方を解説
有効数字とは
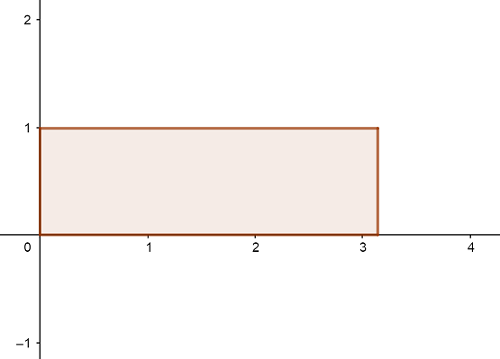
例えば、以下のような目盛りで、物体の横の長さを測ったとします。
実験では目盛りの10分の1までは目分量で読まなければいけませんので、
図の場合、
「3.1cmぐらいかなぁ~」
ということになります。
この小数第1位の「1」の数字には誤差を含んでいるのですが、測定上は有効な数字として認められています。
ですので、上の例の場合、「有効数字2桁(3と1)の数値」といいます。
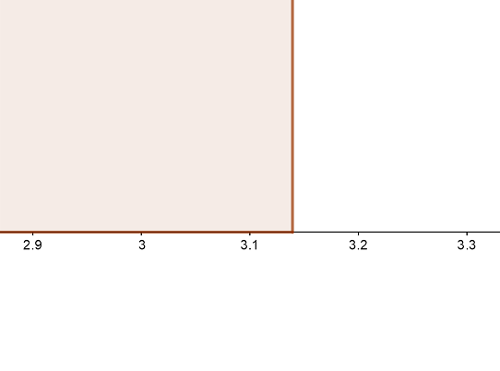
次に、もう少し細かい目盛りで、同じ物体の横の長さを測ってみます。
今度も目盛りの10分の1まで目分量で読み取ると、
「3.14cmなんじゃね?」
と測定され、有効数字は3桁(3,1,4)になるのです。
このように、有効数字はその桁数が多ければ多いほど、より高い精度で測定していると言えるのです。
有効数字の桁数の数え方
先ほど測った「3.14cm」という数値ですが、単位を「m」で表すと、
「0.0314m」
です。
これは「有効数字5桁」と言えるのでしょうか?
……当たり前ですが、言えません。
そもそも、同じ目盛りで測定しているのに、単位を変えただけで精度が上がってしまうのはおかしな話です。
ですので、このようなケースでは、初めに連続している「0」は有効数字に含めず、
「3」以下の3桁を有効数字として扱います。
次に、「3.14cm」の単位を「μm」で表してみましょう。
「31400μm」
となりますが、有効数字が何桁だか分からなくなってしまいますね。
そこで、このような場合では、指数表示を用いて、
$$ 3.14 \times 10^4 \mathrm{({\mu}m)} $$
と記述すれば、有効数字の部分を明確に表現することができるのです。
有効数字の計算
それでは、ここから具体的な有効数字の計算法を見ていきましょう。
足し算と引き算
足し算と引き算では、有効数字の最後の数字が最も高い位にあるものに合わせます。
例えば上の例の場合、赤が誤差を含んでいる数字になるので、
位の最も高い小数第1位に合わせるという意味です。
掛け算と割り算
掛け算と割り算では、有効数字の桁数が最も少ないものに合わせます。
例えば上の例の場合、赤が誤差を含んでいる数字になるので、
桁数の最も少ない2桁に合わせるという意味です。
有効数字n桁で答える場合
問題に、
「有効数字n桁で答えよ」
と指示がある場合は、少々複雑になります。
まず、途中の計算は n+1桁を残してあとは切り捨てます。
最後に n+1桁目を四捨五入し、n桁にするという手順です。
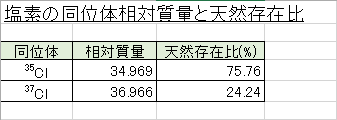
例えば、上のような表をもとに、「塩素の原子量を有効数字3桁で求めよ」という問題があったとします。
このときの計算は、以下のように行います。
$$ 34.969 \times 0.7576 = 26.4925144 $$ → 切り捨てて 26.49 に。
$$ 36.966 \times 0.2424 = 8.9605584 $$ → 切り捨てて 8.960 に。
$$ 26.49 + 8.960 = 35.450 $$ → 四捨五入して 35.5 に。
といった具合です。
まとめ
いかがでしたでしょうか。
高校の定期テストぐらいであれば、有効数字についてそれほど厳しく追求されないと思いますが、
大学の理系学部に進学した場合は、有効数字を正しく扱えるようになる必要があります。
とは言っても、慣れてしまえばそれほど難しくはありませんので、本記事を参考に、
実践での経験を積まれてみてください。
それでは、最後までお読みくださり、ありがとうございました!
おすすめの記事