グラフ理論において、あるグラフが平面的であるかどうかを見極めるための重要な定理、
クラトフスキーの定理
の証明第7弾です。
前回までの記事を読まれていない方は、まずそちらからご覧ください。
- クラトフスキーの定理の証明(1)グラフ理論用語と定理の紹介
- クラトフスキーの定理の証明(2)点連結度から1-連結の証明まで
- クラトフスキーの定理の証明(3)誘導部分グラフから2-連結の証明
- クラトフスキーの定理の証明(4)3-連結の証明と縮約・拡逆
- クラトフスキーの定理の証明(5)3-連結は平面的を証明する準備
- クラトフスキーの定理の証明(6)3-連結は凸埋め込みを持つ証明
前回の記事では、クラトフスキー部分グラフを含まない 3-連結グラフは、
それよりも頂点数が 1つ少ないグラフを拡逆して得られることについて述べました。
6回にわたり連載してきた証明もついに最終回。
前回に引き続き帰納法を進め、クラトフスキーの定理の証明を完結させます。
■ 3-連結グラフが凸埋め込みを持つことの証明(続き)
初めに、記号の定義を再確認しておきます。
・\(z\) … \(G_k\) において拡逆を行う頂点
・\(x\) … \(z\) を拡逆したとき、複製元となる頂点
・\(y\) … \(z\) を拡逆したとき、複製先となる頂点
・\((x_1,\cdots,x_n)\) … \(x\) に隣接した多角形上の頂点
・\((y_1,\cdots,y_n)\) … \(y\) に隣接した多角形上の頂点
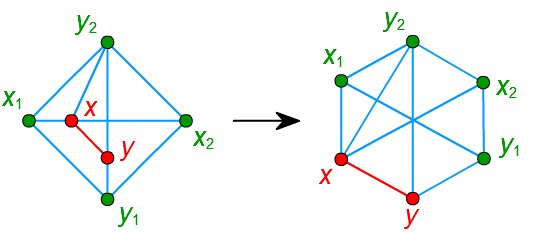
▽ \(y_1,y_2\) が \(x_1,x_2\) の間にあるとき
□ \(G_k\) を拡逆して得られた \(G_{k+1}\) は 3-連結なので、
\(y\) は \(x\) から伸ばされた辺以外に、\(z\) と隣接していた2個以上の頂点と辺で接続されています。
□ \(y\) と隣接する頂点がすべて \(x_1\) と \(x_2\) の間にあるとき(\(x_1\) と \(x_2\) を含みます)、
\(G_{k+1}\) は凸埋め込みを持つので平面的グラフになります。
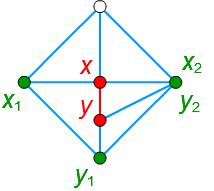
▽ \(x\) と \(y\) が 隣接した頂点を 3個以上共有するとき
□ この時、\(G_{k+1}\) は非平面的グラフになりますが、\(G_{k+1}\) は \(K_5\) の細分を含んでいます。
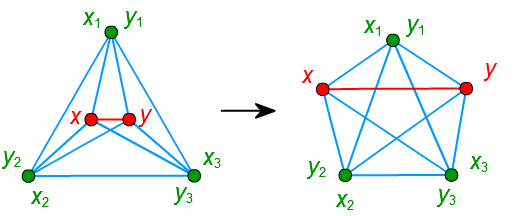
▽ \(x_1,y_1,x_2,y_2\) がこの順で多角形上にあるとき
□ この時も \(G_{k+1}\) は非平面的グラフになりますが、\(G_{k+1}\) は \(K_{3,3}\) の細分を含んでいます。
■ 結論
\(G_{k+1}\) がクラトフスキー部分グラフを含まないことに矛盾しなかったのは、
最初のケースだけであり、その時 \(G_{k+1}\) は凸埋め込みを持ちました。
帰納法より、これは、クラトフスキー部分グラフを持たない 3-連結グラフが全て平面的であることを示しています。
したがって、非平面的グラフには必ず \(K_5\) か \(K_{3,3}\) の細分が含まれているのです。
■ まとめ
いやー、ここまで本当に長かったです。
クラトフスキーの定理の証明を勉強している時、難しくて何度も理解するのを諦めようと思いました。
しかし、行き詰まるたびにグラフ理論の本を読んだり、インターネットで用語を調べたりして、少しずつ前に進んできました。
そこまで頑張ることができたのは、この定理の証明の中に、四色問題を解くための鍵が隠されているのではないかと考えたからです。
そして、自分が学んだことを、こうしてブログの記事という形にできたことをとても嬉しく思います。
この記事が、グラフ理論を学ぶ人々に少しでも役立てば幸いです。
末筆ながら、長い証明に最後までお付き合いくださった読者に感謝いたします。
コメント
学生ですが、本を読んでもわかりにくいクラトフスキーの定理の証明がわかりやすく載っており、とても感動しました。
> たまごさん
コメントありがとうございます。
そう言っていただけると、頑張って書いて良かったなと思えます。
一生懸命ブログを書いても、なかなかアクセスが増えなくて、
モチベーションが下がっていたのですが、もう一度、本当に読者に
喜ばれる記事を、自分自身も楽しみながら書いていこうと思いました。
僕も感動しました。感謝いたします!