グラフ理論において、あるグラフが平面的であるかどうかを見極めるための重要な定理、
クラトフスキーの定理
の証明第3弾です。
前回までの記事を読まれていない方は、まずそちらからご覧ください。
さて、今回は前回に引き続き、最小の非平面的グラフが3-連結になることを証明していきます。
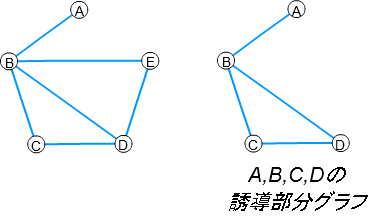
■ 誘導部分グラフ
あるグラフから特定の頂点を指定し、それらの頂点に両端が接続する辺を取り出した部分グラフのことです。
「指定されなかった頂点を辺ごと取り除いた部分グラフ」と考えても差し支えありません。
■ 最小の非平面的グラフが 2-連結 であることの証明
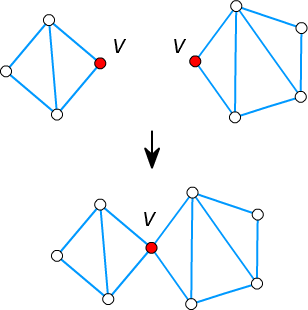
□ 最小の非平面的グラフ \(G\) が 2-連結でない、すなわち 1-連結 であると仮定します。
□ 仮定より、それを取り除くことで \(G\) が非連結となるような頂点 \(v\) が存在します。
□ \(v\) を取り除いた非連結グラフの連結成分の1つを \(C\) とします。
□ \(G\) は最小の非平面的グラフなので、\(C\) と \(v\) の誘導部分グラフと、
\(G-C\) と \(v\) の誘導部分グラフはどちらも平面的になります。
□ すると、双方の \(v\) を合体させることで、\(G\) も平面に描くことができるので、
\(G\) が非平面的であることに矛盾します。
■ 最小の非平面的グラフが 3-連結 であることの準備
▽ 証明
背理法と帰納法を用いて証明します。
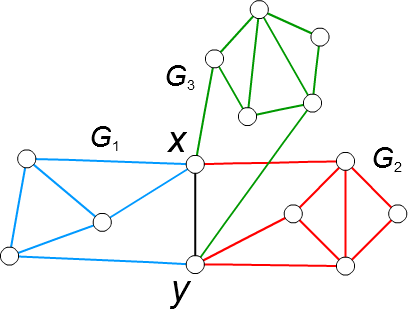
□ \(G\) を \(x,y\) で切断した非連結グラフの連結成分を \(C_1,\cdots,C_k\) とします。
□ \(C_i\) と \(x,y\) の誘導部分グラフに辺 \(xy\) を加えたグラフを \(G_i\) とします。
□ \(G_1,\cdots,G_k\) がすべて平面的であると仮定します。
・ 仮定より、\(G_1\) は平面に(辺の交差なしで)描けます。
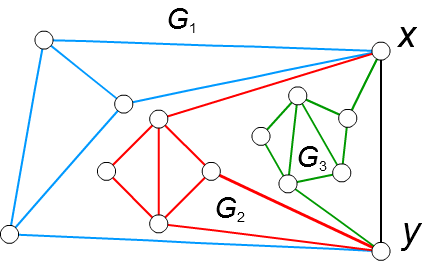
・ \(G_i\) が平面に描けるとき、\(G_{i+1}\) は \(G_i\) の辺 \(xy\) を含む面の中に描くことができ、
2つのグラフを辺 \(xy\) で合体させると、やはり平面グラフになります。
□ このようにして、\(k\) 個のグラフを次々に合体させていくと、\(G\) 全体も平面に描くことができるので、
\(G\) が非平面的であることに矛盾します。
■ まとめ
だんだん難しくなってきましたね。
私も初めてこの証明を読んだときは、何を言っているのかさっぱり分からなくて苦労しました。
「もっと図を使って説明してくれれば理解できるのに…」
とその時思ったものです。
ですので、今回の記事では、できるだけ図を多用して視覚的にイメージできるよう配慮したつもりです。
次回は、いよいよ最小の非平面的グラフが 3-連結であることを証明します。
乞うご期待。
コメント
x-y間に辺がない場合はどうでしょう?
> ブルドーザー富澤さん
コメントありがとうございます。
「x-y間に辺がない場合はどうなるか」については、次の記事で解説していますので、
そちらをご覧ください。
「クラトフスキーの定理の証明(4)3-連結の証明と縮約・拡逆」
https://nayami0425.com/kuratowski_4/