中学数学の公式一覧。図形や関数、計算、方程式、確率まで。

中学の数学で学ぶ公式を、関数や図形などの分野別に一覧にしました。

お気に入りに登録しておくと、必要なときに何度も見られて便利です。

もし気に入っていただけたら、お友達にもこのブログを教えてあげてくださいね！

中学数学の公式一覧。図形や関数、計算、方程式、確率まで。

計算の公式

交換法則・結合法則・分配法則

・加法の交換法則　　\( a+b = b+a \)

・加法の結合法則　　\( a+b+c = (a+b)+c = a+(b+c) \)

・乗法の交換法則　　\( ab = ba \)

・乗法の結合法則　　\( abc = (ab)c = a(bc) \)

・分配法則　　\( (a+b) \times c = c \times (a+b) = ac+bc \)

等式の性質

\( A = B \) が成り立つとき、

・和　　\( A+C = B+C \)

・差　　\( A-C = B-C \)

・積　　\( AC = BC \)

・商　　\( \displaystyle \frac{A}{C} = \displaystyle \frac{B}{C} \)　　\( (C \neq 0) \)

指数法則

・\( a^m \times a^n = a^{m+n} \)

・\( (a^m)^n = a^{mn} \)

・\( (ab)^m = a^mb^m \)

展開・因数分解

・\( (a+b)(c+d) = ac+ad+bc+bd \)

・\( (x+a)(x+b) = x^2+(a+b)x+ab \)

・\( (a+b)^2 = a^2+2ab+b^2 \)

・\( (a-b)^2 = a^2-2ab+b^2 \)

・\( (a+b)(a-b) = a^2-b^2 \)

・\( (ax+b)(cx+d) = acx^2+(ad+bc)x+bd \)

平方根

・\( (\sqrt{a})^2 = a \)

・\( \sqrt{a^2} = |a| \)　　( \(|a|\) は \(a\) の絶対値)

・\( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \)

・\( \displaystyle \frac{\sqrt{b}}{\sqrt{a}} = \sqrt{\displaystyle \frac{b}{a}} \)

二次方程式の解の公式

・\( ax^2+bx+c=0 \) の解　　\( x = \displaystyle \frac{ -b \pm \sqrt{b^2-4ac} }{2a} \)

・\( ax^2+2b’x+c=0 \) の解　　\( x = \displaystyle \frac{-b’ \pm \sqrt{b’^2-ac} }{a} \)

関数の公式

比例

・\( y = ax \)　　(\(a\):比例定数)

反比例

・\( y = \displaystyle \frac{a}{x} \)　　(\(a\):比例定数)

一次関数

・\( y = ax + b \)　　(\(a\):傾き　\(b\):切片)

・2直線が平行 \( \Rightarrow \) 2直線の傾きが等しい

・2直線が垂直 \(\Rightarrow\) 2直線の傾きをかけると \(-1\)

関数 y = ax^2

・\( y = ax^2 \)　　(\(a\):比例定数)

変化の割合

・\( 変化の割合 = \displaystyle \frac{yの増加量}{xの増加量} \)

・\( y = ax \) の変化の割合　　\( a \)

・\( y = \displaystyle \frac{a}{x} \) の変化の割合　　\( – \displaystyle \frac{a}{pq} \)　　(\(x\) が \(p\) から \(q\) まで変化するとき)

・\( y = ax+b \) の変化の割合　　\( a \)

・\( y = ax^2 \) の変化の割合　　\( a(p+q) \)　　(\(x\) が \(p\) から \(q\) まで変化するとき)

直線と放物線

 

 

放物線 \(y=ax^2\) と直線が2点で交わるとき、二つの交点の \(x\) 座標をそれぞれ、\(p, q\) とすると、直線の式は、

・傾き　　\( a(p+q) \)

・切片　　\( -apq \)

で表される。

図形の公式

円の公式

・\( l = 2 \pi r \)　　(\(l\):円周　\(r\):半径)

・\( S = \pi r^2 \)　　(\(S\):円の面積　\(r\):半径)

おうぎ形の公式

・\( l = 2 \pi r \times \displaystyle \frac{a}{360} \)　　(\(l\):弧の長さ　\(r\):半径　\(a\):中心角)

・\( S = \pi r^2 \times \displaystyle \frac{a}{360} \)　　(\(S\):おうぎ形の面積　\(r\):半径　\(a\):中心角)

・\( S = \displaystyle \frac{1}{2} lr \)　　(\(S\):おうぎ形の面積　\(l\):弧の長さ　\(r\):半径)

角柱・円柱の公式

・表面積 \(=\) 側面積 \(+\) 底面積 \(\times 2\)

・側面積 \(=\) 底面の周 \(\times\) 高さ

・\( V = Sh \)　　(\(V\):体積　\(S\):底面積　\(h\):高さ)

角錐・円錐の公式

・表面積 \(=\) 側面積 \(+\) 底面積

・\( a = 360^\circ \times \displaystyle \frac{r}{l} \)　　(\(a\):側面のおうぎ形の中心角　\(l\):母線　\(r\):半径)

・円錐の側面積 \(= \pi lr \)　　(\(l\):母線　\(r\):半径)

球の公式

・\( S = 4 \pi r^2 \)　　(\(S\):表面積　\(r\):半径)

・\( V = \displaystyle \frac{4 \pi r^3}{3} \)　　(\(V\):体積　\(r\):半径)

平行線と角

・対頂角は等しい

・2直線が平行 \(\Leftrightarrow\) 同位角が等しい

・2直線が平行 \(\Leftrightarrow\) 錯角が等しい

多角形

・n角形の内角の和　　\( 180^\circ \times (n-2) \)

・n角形の外角の和　　\( 360^\circ \)

三角形の合同条件

・3組の辺がそれぞれ等しい

・2組の辺とその間の角がそれぞれ等しい

・1組の辺とその両端の角がそれぞれ等しい

直角三角形の合同条件

・斜辺と一つの鋭角がそれぞれ等しい

・斜辺と他の1辺がそれぞれ等しい

二等辺三角形

・二等辺三角形の底角は等しい

・二つの角が等しい三角形は二等辺三角形である

・頂角の二等分線は底辺を垂直に二等分する

平行四辺形の性質

・2組の対辺がそれぞれ等しい

・2組の対角がそれぞれ等しい

・対角線がそれぞれの中点で交わる

平行四辺形になる条件

・2組の対辺がそれぞれ平行である

・2組の対辺がそれぞれ等しい

・2組の対角がそれぞれ等しい

・対角線がそれぞれの中点で交わる

・1組の対辺が平行でその長さが等しい

三角形の相似条件

・3組の辺の比がすべて等しい

・2組の辺の比とその間の角がそれぞれ等しい

・2組の角がそれぞれ等しい

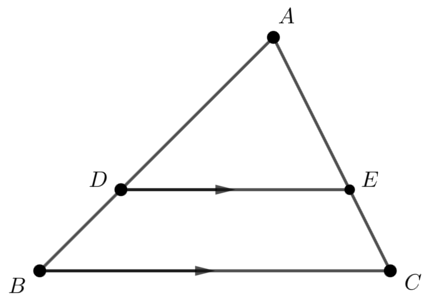
相似の基本パターン

・ピラミッド型　　\( AD:AB = AE:AC = DE:BC \)

 

 

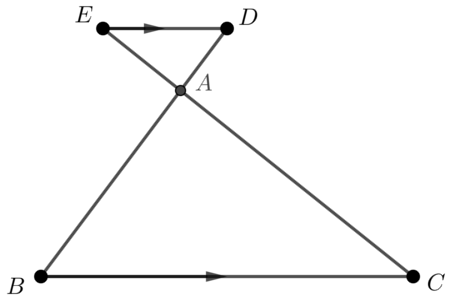
・砂時計型　　\( AD:AB = AE:AC = DE:BC \)

 

 

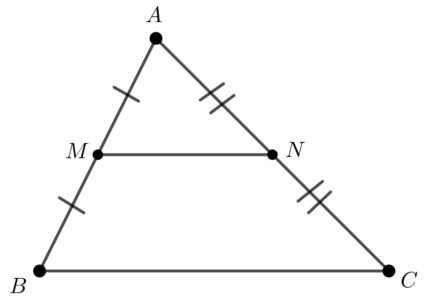
中点連結定理

\( M, N \) を辺の中点とすると、

・\( MN \parallel BC \)　　(\(\parallel\):平行)

・\( MN = \displaystyle \frac{1}{2}BC \)

 

 

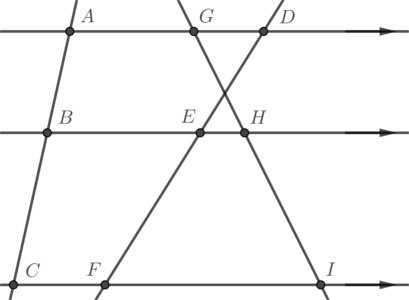
平行線と線分の比

・平行線によって分けられる線分の比はどこも等しい　　\( AB:BC = DE:EF = GH:HI \)

 

 

相似な図形の面積比・体積比

二つの図形の相似比が \(m:n\) であるとき、

・面積比　　\(m^2:n^2\)

・体積比　　\(m^3:n^3\)

円周角の定理

・同じ弧に対する円周角の大きさは等しい

・同じ弧に対する円周角の大きさは中心角の大きさの半分である

・半円の弧に対する円周角の大きさは\( 90^\circ \)である

円の接線・弦

・円の接線は接点を通る半径に垂直である

・円の弦の垂直二等分線は円の中心を通る

・円外の点から円に引いた接線の長さは等しい

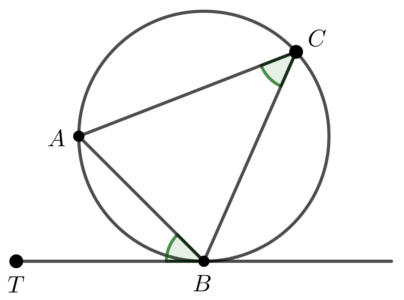
接弦定理

・\( \angle ABT = \angle ACB \)

 

 

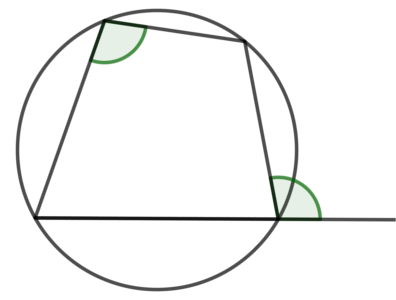
円に内接する四角形

・円に内接する四角形の対角の和は\( 180^\circ \)である

・円に内接する四角形の外角は、それと隣合う内角の対角に等しい

 

 

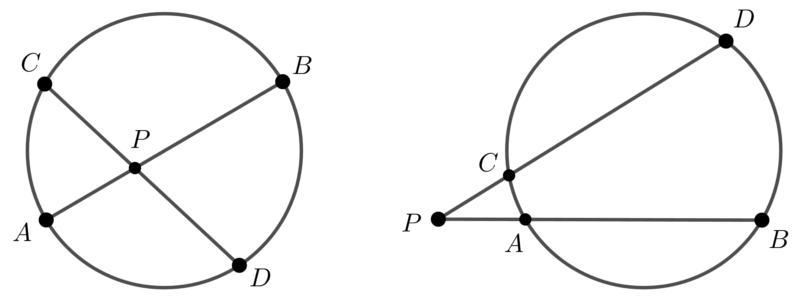
方べきの定理

・平行でない2直線が円とそれぞれ2点で交わるとき

\( PA \times PB = PC \times PD \)

 

 

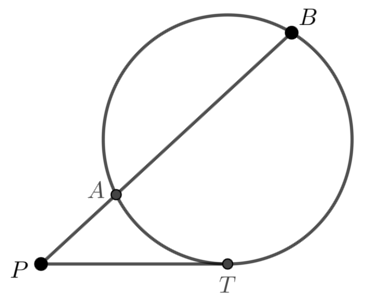
・平行でない2直線のうち、1本が円と2点で交わり、もう1本が円と接するとき

\( PA \times PB = PT^2 \)

 

 

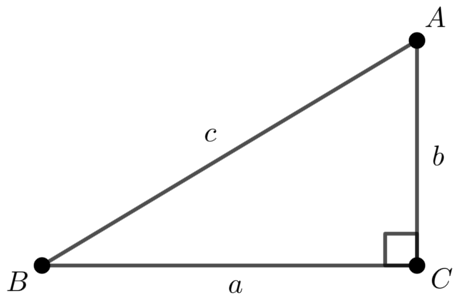
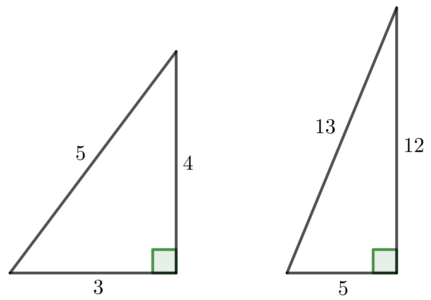
三平方の定理

・\( a^2+b^2=c^2 \)

 

 

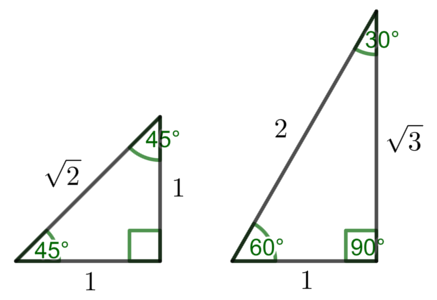
特別な直角三角形の辺の比

 

 

 

正三角形の面積

・\( S = \displaystyle \frac{\sqrt{3}}{4}a^2 \)　　(\(S\):面積　\(a\):1辺の長さ)

直方体・立方体の対角線

・直方体の対角線の長さ　　\( \sqrt{a^2+b^2+c^2} \)　　(\(a\):縦　\(b\):横　\(c\):高さ)

・立方体の対角線の長さ　　\( \sqrt{3}a \)　　(\(a\):1辺の長さ)

正四面体

・体積　　\( V = \displaystyle \frac{ \sqrt{2} }{12}a^3 \)　　(\(V\):体積　\(a\):1辺の長さ)

場合の数・確率の公式

組合せ

・n個のものから2個を選ぶ選び方　　\( \displaystyle \frac{n(n-1)}{2 \times 1} \)

・n個のものから3個を選ぶ選び方　　\( \displaystyle \frac{n(n-1)(n-2)}{3 \times 2 \times 1} \)

確率

・Pが起こらない確率　　\( 1-p \)　　(\(p:P\) が起こる確率)

・少なくとも1回以上Pが起こる確率　　\(1-\) (1回も \(P\) が起こらない確率)