グラフ理論において、あるグラフが平面的であるかどうかを見極めるための重要な定理、
クラトフスキーの定理
の証明第6弾です。
前回までの記事を読まれていない方は、まずそちらからご覧ください。
- クラトフスキーの定理の証明(1)グラフ理論用語と定理の紹介
- クラトフスキーの定理の証明(2)点連結度から1-連結の証明まで
- クラトフスキーの定理の証明(3)誘導部分グラフから2-連結の証明
- クラトフスキーの定理の証明(4)3-連結の証明と縮約・拡逆
- クラトフスキーの定理の証明(5)3-連結は平面的を証明する準備
前回と前々回の記事では、
従属命題 A
従属命題 B
という2つの従属命題を証明しました。
今回はその従属命題を用いて、いよいよクラトフスキーの定理の証明を完結させていこうと思います。
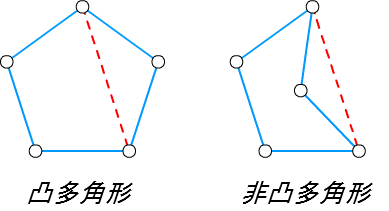
■ 凸多角形
凸多角形 とは、どの 2頂点を結ぶ線分も、その多角形の外に出ることがないようなものです。
凸多角形では、どの内角の大きさも \(180^\circ\) 未満になっています。
■ 凸埋め込み
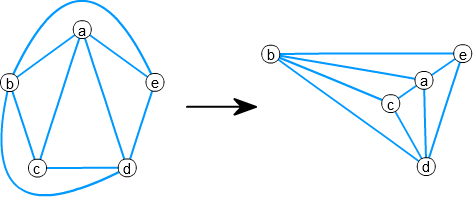
平面的グラフ \(G\) の 凸埋め込み とは、すべての辺がまっすぐな線分で、
一番外側を除くすべての面が凸多角形であるような平面グラフです。
■ 3-連結グラフが凸埋め込みを持つことの証明
その時、\(G\) は凸埋め込みを持つ。
これは、\(G\) が平面的であることを示し、こうしてクラトフスキーの定理の証明が完結します。
上の命題を頂点数についての帰納法で証明します。
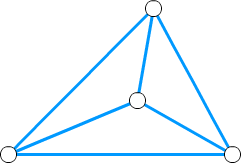
帰納法の基礎
最小の 3-連結グラフは 4個の頂点を持ちます。
帰納法のステップ
□ \(k\) を4以上の自然数、頂点数 \(|V|=k\) のクラトフスキー部分グラフを含まない 3-連結グラフを \(G_k\) とします。
□ 従属命題 A より、\(|V|=k+1\) のとき、縮約しても 3-連結になるような辺 \(e\) が存在します。
□ 従属命題 B より、クラトフスキー部分グラフを拡逆しても、クラトフスキー部分グラフを含まないグラフは生成できません。
以上のことから、\(G_{k+1}\) は \(G_k\) を拡逆して生成可能であることが分かります。
□ \(G_k\) が平面的であるとき、\(G_{k+1}\) も平面的であるかどうかを調べていきます。
□ \(G_k\) において、拡逆を行う頂点を \(z\) とします。
□ \(G_k\) は 3-連結なので、\(z\) を取り除いても 2-連結以上となり、
\(z\) は多角形の中に存在することになります。
□ \(z\) を拡逆したとき、複製元となる頂点を \(x\)、複製先となる頂点を \(y\) とします。
□ また、\(x\) に隣接した多角形上の頂点を \(x_1,\cdots,x_n\)、\(y\) に隣接した頂点を \(y_1,\cdots,y_n\) とします。
■ まとめ
まだ帰納法の途中ですが、記事が長くなってきたので続きは次回にしたいと思います。
ここまで6回にわたり連載してきたクラトフスキーの定理の証明もいよいよ最終回。
クラトフスキー部分グラフを含まない 3-連結グラフは凸埋め込みを持つ(=平面的である)ことを示し、
非平面的グラフを生成するには、やはりクラトフスキー部分グラフを含めなければならないという結論を導きます。
読者と一緒に感動の結末を迎えたいので、次回の記事もどうぞよろしくお願いいたします。
次の記事 → クラトフスキーの定理の証明(7)そして完結へ
コメント
Gkは3-連結なので、zを取り除くと2-連結となり、
「zは多角形の中に存在することになります。」
という部分の理由がわかりません。コメントいただけると嬉しいです。
コメントありがとうございます。
早速ですが、ご質問に回答させていただきます。
まず、Gkは頂点の数がk個の3-連結グラフです。
3-連結ということは、頂点を3個以上取り除かなければ、グラフを非連結にできません。
そのGkからzという頂点を取り除いたとすると、少なくともあと2個以上頂点を取り除かなければグラフは非連結になりません。
ですので、zを取り除いたグラフは少なくとも2-連結以上になっているはずです。
ここで『クラトフスキーの定理の証明(2)』をもう一度見てみると、2-連結以上のグラフは「ハミルトンサイクル」を持つので、全ての頂点が輪の形で並んでいる、すなわち多角形に変形することができます。
よって、多角形に変形した後に、再び頂点zをグラフに戻せば、zが多角形の中にある形で表現できるということです。
難しい証明なのに、ここまで読み進めてくださり、とても嬉しく思います。
それでは、お勉強、頑張られてください!
ハミルトンサイクルを持つグラフは2-連結以上ですが、2ー連結以上だからといってハミルトンサイクルを持つわけではないので、2ー連結以上ならば多角形に変形できるとはいえないのではないでしょうか?
> 素数さん
コメントありがとうございます。
そして、返信が遅くなり申し訳ございませんでした。
「2ー連結以上だからといってハミルトンサイクルを持つわけではない」
というのは、まさに素数さんのおっしゃる通りで、2020年6月8日に書いた私のコメントは間違っていることになります。
改めて調べたのですが、グラフの連結度については Menger’s theorem(メンガーの定理)というものがあり、これは、
「2点連結のグラフは、あらゆる頂点間に2つ以上の独立した(内部で頂点を共有しない)パスを持つ」
というものです。
Gkは3点連結なので、zの次数は3以上です。
zと隣接する頂点をa, b, cとします。
Gk-zは2点連結なので、ab間やbc間にはパスが存在します。
[1] abパスとbcパスが独立している場合
cからbを通ってaに行くことができますが、メンガーの定理より、これとは別のcaパスが存在します。
これはabcを通るサイクル、すなわちabcを頂点とする多角形が存在することを表します。
[2] abパスとbcパスが独立していない場合
例えば、bcパスがaを共有している(aを通る)ような場合です。
この場合もメンガーの定理より、bからcに行く別のパスが存在するのでやはりabcを通るサイクルが存在することになります。
Q.E.D.
3-連結グラフBに適当な3頂点と接する頂点zを追加してできるグラフをGとした時、Gは3-連結でzを取り除いても3-連結のままになるので「Gkは3-連結なので、zを取り除くと2-連結となり」というのは自明ではないんじゃないですか
> 合成数さん
コメントありがとうございます。
合成数さんのおっしゃる通りです。
「Gkは3-連結なので、zを取り除いても2-連結以上となり」が正しい表現でした。
記事もそのように訂正しておきたいと思います。
ご指摘ありがとうございました!