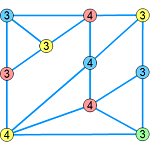
彩色数と次数の定理(グラフ理論)
数学のグラフ理論の分野でグラフの彩色数と頂点の次数に関する定理を見つけたのでブログの記事にしました。
毎日のふとした困り事。その解決法がここにあるかもしれません。

数学のグラフ理論の分野でグラフの彩色数と頂点の次数に関する定理を見つけたのでブログの記事にしました。
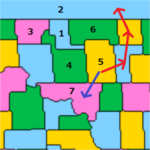
四色問題の塗り絵パズルアプリで、周りを4色で囲まれてしまい、行き詰まった時の対処法をお教えします。
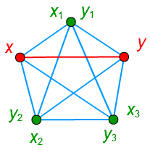
クラトフスキーの定理の証明第7弾。3-連結グラフが平面的であることを示し、ついに証明が完結します。
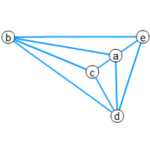
クラトフスキーの定理の証明第6弾。凸多角形の説明と、3-連結グラフが凸埋め込みを持つ証明。
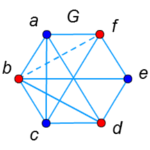
クラトフスキーの定理の証明第5弾。3-連結グラフが平面的になることを証明するための準備です。
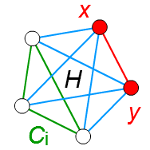
クラトフスキーの定理の証明第4弾。非平面的グラフが3-連結である証明と、縮約・拡逆の説明
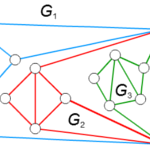
クラトフスキーの定理の証明第3弾。誘導部分グラフの説明と最小の非平面的グラフが2-連結である証明
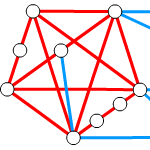
クラトフスキーの定理の証明第2弾。点連結度の解説と最小の非平面的グラフが1-連結である証明まで。
完全グラフ、細分、位相的マイナーといった用語を解説し、クラトフスキーの定理を紹介しています。

四色問題の証明にあたり、双対グラフや平面グラフ、オイラーの多面体定理について解説しています。