クラトフスキーの定理の証明（1）グラフ理論用語と定理の紹介

グラフ理論において、あるグラフが平面的であるかどうかを判定するための重要な定理があります。

それは、

 

クラトフスキーの定理

 

です。

 

このクラトフスキーの定理ですが、なぜこのような定理が成り立つのか、

インターネットや本で調べてもなかなか証明が出てこないんですよね。

 

定理自体は紹介されていても、証明については、

 

「難しいので省略します」

 

と。

 

「いや、いや、そこが知りたいんですけど！」

 

みたいな。

 

であれば、この際、自分がクラトフスキーの定理の証明を分かりやすく解説しようと思い立ったわけです。

クラトフスキーの定理の証明を知りたい人が日本で何人いるのかよく分かりませんが、もうアクセス数とかどうでもいいんです。

 

「日本で最初にクラトフスキーの定理の証明を分かりやすく解説したサイトを作成した」

 

これが重要なんです。

そして、自分の書いた記事が、グラフ理論を勉強する人たちの役に立てばそれで十分だと。

前置きが長くなりましたが、早速行きましょう。

 

• グラフ理論の双対グラフ、平面グラフと平面的グラフ、オイラーの定理

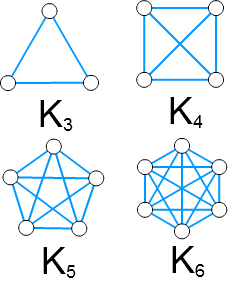
■ 完全グラフ \(K_n\)

完全グラフ \(K_n\) とは、頂点が \(n\) 個あり、すべての2頂点間に辺があるグラフのことです。

 

 

■ 二部グラフ、完全二部グラフ \(K_{m,n}\)

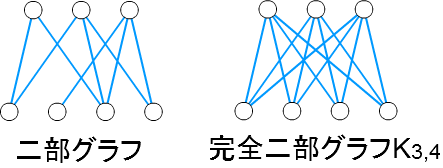
二部グラフとは、頂点が2つのグループに分けられ、同じグループの頂点同士は辺で結ばれていないグラフのことです。

完全二部グラフ \(K_{m,n}\) とは、\(m\) 個の頂点グループと \(n\) 個の頂点グループがあり、異なるグループのすべての2頂点間に辺がある二部グラフのことです。

 

 

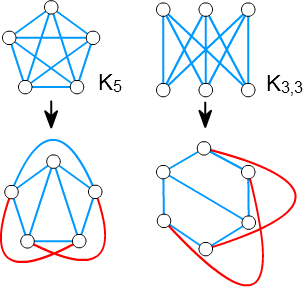
■ 最小の非平面的グラフ

完全グラフ \(K_5\) と完全二部グラフ \(K_{3,3}\) は、非平面的グラフであることが知られています。

 

 

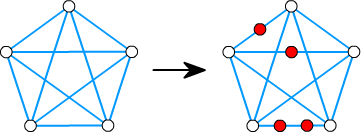
■ 細分

細分とは、グラフの辺上に新たな頂点を0個以上加えて作ったグラフのことです。

ちなみに、\(K_5\) や \(K_{3,3}\) を細分しても、それらを平面的グラフにすることはできません。

もし、細分して平面グラフになるなら、細分で加えた頂点を消去することで元のグラフも平面で描けることになってしまうからです。

 

 

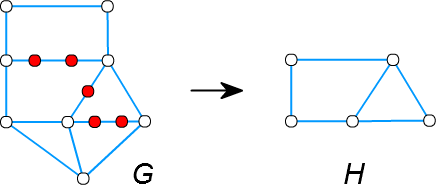
■ 位相的マイナー

グラフ \(G\) がグラフ \(H\) の細分を部分グラフに含んでいるとき、

「 \(H\) は \(G\) の位相的マイナーである」

といいます。

 

 

■ クラトフスキーの定理

 

グラフに \(K_5\) や \(K_{3,3}\) が部分グラフとして含まれていたら、

そのグラフは平面的グラフにはならないので（もし平面になるなら、\(K_5\) や \(K_{3,3}\) も平面になってしまう）、

左から右の証明は何となく理解できると思います。

 

難しいのは、右から左、すなわち、

「あらゆる非平面的グラフは \(K_5\) や \(K_{3,3}\) の位相的マイナーを含む」

ことの証明です。

■ まとめ

クラトフスキーの定理を証明する記事の第1弾は、定理を紹介するだけで終わってしまいました。

まあ、それなりに難しい定理ですからねぇ。

次回は、いよいよ定理の証明に入っていきます。

お楽しみに！

 

次の記事　→　クラトフスキーの定理の証明（2）点連結度から1-連結の証明まで